一些数论公式

斯特灵公式是一条用来取n阶乘近似值的数学公式。一般来说，当n很大的时候，n阶乘的计算量十分大，所以斯特灵公式十分好用，而且，即使在

n很小的时候，斯特灵公式的取值已经十分准确。

公式为：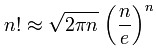

以下等式或者不等式均可以用数学归纳法予以证明！

1 + 3 + 5 + ... + (2n - 1) = n^2

1*2 + 2*3 + 3*4 + ... + n*(n + 1) = n*(n + 1)*(n + 2) / 3

1*1! + 2*2! + 3*3! + ... + n*n! = (n + 1)! - 1

1^2 + 2^2 + 3^2 + ... + n^2 = n*(n + 1)*(2n + 1) / 6

1^2 - 2^2 + 3^2 -... + (-1)^n * n^2 = (-1)^(n + 1) * n * (n + 1) / 2

2^2 + 4^2 + ... + (2n)^2 = 2n*(n+1)*(2n+1) / 3

1/2! + 2/3! + ... + n/(n+1)! = 1 - 1/(n+1)!

2^(n + 1) < 1 + (n + 1)2^n

1^3 + 2^3 + 3^3 + ... + n^3 = (n*(n + 1) / 2)^2

1/2n <= 1*3*5*...*(2n-1) / (2*4*6*...*2n) <= 1 / sqrt(n+1)<wbr>n=1,2...</wbr>

2^n >= n^2 , n=4, 5,...

2^n >= 2n + 1, n=3,4,...

r^0 + r^1 + ... + r^n < 1 / (1 - r), n>=0, 0<r<1

1*r^1 + 2*r^2 + ... + n*r^n < r / (1-r)^2, n>=1, 0<r<1

1/2^1 + 2/2^2 + 3/2^3 + ... + n /2^n < 2, n>=1

<wbr></wbr>

5^n - 1能被4整除

7^n - 1能被6整除

11^n - 6能被5整除

6*7^n - 2*3^n能被4整除

3^n + 7^n - 2能被8整除

<wbr></wbr>

n条直线能将平面最多划分为(n^2 + n + 2) / 2个区域

定义H(k) = 1 + 1/2 + 1/3 + ... + 1/k 则 1 + n/2 <=H(2^n) <= 1 + n

H(1) + H(2) + ... + H(n) = (n + 1) * H(n) - n

1*H(1) + 2*H(2) + ... + n*H(n) = n*(n + 1) / 2 * H(n + 1) - n * (n + 1) / 4

欧拉函数的定义:E(k)=([1,n-1]中与n互质的整数个数).因为任意正整数都可以唯一表示成如下形式:
k=p1^a1*p2^a2*……*pi^ai;(即分解质因数形式)
可以推出:E(k)=(p1-1)(p2-1)……(pi-1)*(p1^(a1-1))(p2^(a2-1))……(pi^(ai-1))
<wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>=k*(p1-1)(p2-1)……(pi-1)/(p1*p2*……pi);<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>=k*(1-1/p1)*(1-1/p2)....(1-1/pk)</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>

在程序中利用欧拉函数如下性质，可以快速求出欧拉函数的值(a为N的质因素)
若(N%a==0 && (N/a)%a==0) 则有:E(N)=E(N/a)*a;
若(N%a==0 && (N/a)%a!=0) 则有:E(N)=E(N/a)*(a-1);

若N>2, 欧拉函数E(N)必定是偶数
若gcd(a,b) = 1,则有E(a * b) = E(a) * E(b)

若一个数N分解成p1^a1 * p2^a2 * ... * pn^an，那么
E(N) = p1^(a1 - 1) * (p1 - 1) * ... * pn^(an - 1) * (pn - 1)

若N>1,不大于N且与N互素的所有正整数的和是1/2 * N * E(N)

因子和: 若 k=p1^a1*p2^a2...*pi^ai<wbr><wbr>F(k) = (p1^0+...+p1^a1)*(p2^0+...+p2^a2)*...*(pi^0 + ... + pi^ai)<br><wbr></wbr></wbr></wbr>

没有一个平方数是以2,3,7,8结尾的

max{a, b, c} - min{a, b, c} = (|a - b| + |b - c| + |a - c|) / 2

ac % m = bc % m 可以得到 a % m' = b % m'<wbr>m' = m / gcd(m, c)</wbr>

如果a % mi = b % mi (i=1,2,...,n) 并且 l = lcm(m1, m2, ..., mn)<wbr>则可以得到 a % l = b % l</wbr>

Euler 定理
若gcd(a,m)==1, 则a^(phi(m)) % m = 1 % m
Fermat小定理
p为素数，对任意的a有 a^p % p = a % p
p为素数 ，对任意的a(a<p), a^(p-1) % p = 1 % p
p为素数 ， 对任意的a，若gcd(p,a)==1, a^(p-1) % p = 1 % p

一个奇数a的平方减1都是8的倍数

任意4个连续整数的乘积再加上1 一定是完全平方数

当a是整数时，a(a-1)(2a-1)是6的倍数

当a是奇数时,<wbr><wbr>a(a^2 - 1)是24的倍数</wbr></wbr>

n次代数方程 x^n + a1 * x^(n-1) + ... + an-1*x + an = 0 的系数都是a1, a2, ... , an都是整数。
如果它有有理数的根，证明这个根一定是整数，而且这个数一定是an的因子。如果不是整数，就一定是无理数。

设a,b都是正整数，a<b而gcd(a,b) = 1 ,如果存在一个素数p，它能够整除b，但是不能够整除10，则a/b一定不能够化成有限小数。如果b=2^a * 5^b，其中a,b都是非负整数，则a/b能化成有限小数。

设0<a<b, 且gcd(a,b) = 1, 如果a/b能表示成纯循环小数，则我们有gcd(b, 10) = 1。

设0<a<b, 且gcd(a,b) = 1, 令h是一个最小的正整数，使得10^h 与1 关于b同余，那么a/b可以表示成纯循环小数
0.d1d2d3...dh。

设b是一个正整数且gcd(10, b) = 1，令h是一个最小的正整数，能使得10^h 与1 关于b同余，则h能够整除Euler(b)

设a, b, b1都是正整数，a < b, gcd(a, b) = 1, b1 > 1, gcd(b1, 10) = 1。b = 2^c * 5^d * b1, 其中c， d都是非负整数，且不同时为0， 令h是一个最小的正整数，使得 10^h 与1 关于b1同余, 则当c>=d时，我们有a/b = 0.a1a2...aca'(c+1)...a'(c + h)<wbr>，而当c &lt; d时，我们有a/b = 0.a1a2...ada'(d+1)...a'(d + h)</wbr>

设0.a1a2...an...不能换成有限小数，也不能化成循环小数，则它不能化成分数。

设p是一个素数，m是一个正整数且m=na+b其中a是一个非负整数而b是一个不大于n-1的非负整数。令
a=p^m, 当b=0的时候，a的开n次方是一个整数，当1<= b <= n - 1时，a的开n次方不能表示为分数。

设p是一个素数，m是一个正整数且m=na+b其中a是一个非负整数而b是一个不大于n-1的非负整数。令
a=p^m, 当b=0的时候，a的开n次方是一个整数，当1<= b <= n - 1时，a的开n次方=b+c, 其中b是一个正整数而c是一个无限小数但不是循环小数。

设a是一个正整数, 当a的开n次方=b+c中b是一个正整数而0<c<1时，则a的开n次方不能表示成为分数，并且这时c是一个无限小数但不是循环小数。

(4b^3 + 3b) / (4b^2 + 1) <= b + 1 / (2b + 1/2b) <=<wbr>根号b平方+1 &lt;= b + 1 / (2b + 1/(2b + 1 / 2b)) = (8b^4 + 8b^2 + 1) / (8b^3 + 4b)</wbr>

b + 1/(2b + 1/(2b + 1/(2b + 1/2b))) <= 根号b平方+1

(16b^5 + 20b^3 + 5b) / (16b^4 + 12b^2 + 1) <= 根号b平方+1 <= (8b^4 + 8b^2 + 1) / (8b^3 + 4b)

<wbr></wbr>

8*8棋盘2牌的完美覆盖数目为12988816=2^4 * 901^2

<wbr></wbr>

一张m行n列棋盘有一个b-牌的完美覆盖，当且仅当b是m的一个因子或者b是n的一个因子

<wbr></wbr>

n阶幻方的幻和为 n*(n^2+1) / 2<wbr><wbr>n阶幻方体的幻和为(n^4+n) / 2</wbr></wbr>

<wbr></wbr>

鸽巢原理： 如果n+1个物体被放进n个盒子，那么至少有一个盒子包含两个或者更多的物体

鸽巢原理加强形式： 令q1，q2，..，qn为正整数。如果将 q1+q2+...+qn-n+1 个物体放入n个盒子内，那么，至少第一个盒子至少含有q1个物体，或者第二个

盒子至少含有q2个物体，... ，或者第n个盒子至少含有qn个物体

<wbr></wbr>

给定m个整数a1,a2,...,am，存在整数p和q，0<=p<q<=m,使得a(p+1)+a(p+2)+...+a(m)能够被m整除。通俗的说，就是在序列a1,a2,...,am中存在连续

个a，使得这些a的和能被m整除

<wbr></wbr>

由n^2+1个实数构成的序列a1，a2,...,a(n^2+1)或者含有长度为n+1的递增子序列，或者含有长度为n+1的递减子序列

<wbr></wbr>

Ramsey定理：在6个（或更多的）人中，或者有3个人，他们中的每两个人都互相认识；或者有3个人，他们中的每两个人都彼此不认识

<wbr></wbr>

n个元素的集合的循环r-排列的个数由

A(n,r)/r=n!/(r * (n-r)!)给出。特别地，n个元素的循环排列的个数是(n-1)!

<wbr></wbr>

多重集排列：

令S是一个多重集，有k个不同类型的元素，各元素的重数分别为n1,n2,...,nk。设S的大小为n=n1+n2+...+nk。则S的排列数等于n!/(n1!*n2!*...*nk!)

<wbr></wbr>

多重集的组合：

令S为具有k中类型元素的一个多重集，每种元素均具有无限的重复数。则S的r-组合的个数等于 C(r+k-1,r)

<wbr></wbr>

如果排列P1P2...Pn有逆序列b1,b2,...,bn，且k=b1+b2+...+bn为逆序数，那么P1P2...Pn可以通过k次连续交换得到12...n

<wbr></wbr>

利用反射Gray码生成相邻元组1的个数相差1的所有组合

<wbr></wbr>

生成{1,2,...,n}的字典序r-组合的算法：

从r-组合a1a2...ar=12..r开始

当a1a2...ar不等于（n-r+1)(n-r+2)...n时,做：

i)确定最大的整数k，是的ak + 1<=n且ak + 1不等于a1,a2,...ar

ii)用r-组合<wbr><wbr>a1...a(k-1)(ak + 1)(ak+2)...(ak + r - k + 1)替换 a1a2...ar</wbr></wbr>

<wbr></wbr>

C(n,k)=C(n-1,k)+C(n-1,k-1)<wbr>1&lt;=k&lt;=n-1</wbr>

<wbr></wbr>

k * C(n,k) = n * C(n-1, k-1)

<wbr></wbr>

C(n,0)+C(n,1)+...+C(n,n) = 2^n<wbr><wbr><wbr>C(n,0)+C(n,2)+... = 2^(n-1)<wbr>C(n,1)+C(n,3)+...=2^(n-1)</wbr></wbr></wbr></wbr>

<wbr></wbr>

1*C(n,1)+2*C(n,2)+...+n*C(n,n)=n*2^(n-1) (n>=1)

<wbr></wbr>

通过对等式 (1+x)^n=sigma(C(n,k)*x^k)<wbr>k: 0-&gt;n 两边就微分，可以得到 sigma(k^p * C(n,k)) k: 1-&gt;n的和</wbr>

<wbr></wbr>

sigma(C(n,k)^2) = C(2n,n)<wbr>k:<wbr>1-&gt;n</wbr></wbr>

<wbr></wbr>

C(r,0)+C(r+1,1)+...+C(r+k,k) = C(r+k+1,k)

<wbr></wbr>

C(0,k)+C(1,k)+...+C(n-1,k)+C(n,k)=C(n+1,k+1)

<wbr></wbr>

Dilworth定理：<wbr>令(X,&lt;=)是一个有限偏序集，并令m是反链的最大大小。则X可以被划分成m个但不能再少的链</wbr>

同理， 若r是链的最大大小，那么X可以被划分成r个但不能再少的反链。

<wbr></wbr>

卷积定理： 对任意两个长度为n的向量a和b，其中n是2的幂，

a,b的卷积等于 (DFT2n)-1(DFT2n(a) . DFT2n(b))

其中向量a和b是用0扩充使其长度达到2n，"."表示2个2n个元素组成的向量的点乘

<wbr></wbr>

18014398509481931 素数
18014398509482111 最小质因子为11
1637672591771101 最小质因子为6780253

<wbr></wbr>

中线定理（pappus定理）是指三角形ABC内BM=MC,则AB^2+AC^2=2*(AM^2+BM^2)

证明：
AC^2=AH^2+HC^2?
AB^2=AH^2+BH^2=AH^2+(HC+2MH)^2=AH^2+HC^2+4MH*HC+4MH^2
左边=AB^2+AC^2=2*AH^2+2CH^2+4MH*CH+4MH^2
右边=2*(AM^2+BM^2)=2*(AH^2+MH^2+(CH+MH)^2)=2*(AH^2+MH^2+CH^2+2CH*MH+MH^2)
得证

<wbr></wbr>

[modified from &豪's blog]
(1)定理:设x0,x1,x2,...是无穷实数列,xj>0,j>=1,那么,
<wbr><wbr><wbr><wbr><wbr>(i)对任意的整数 n&gt;= 1, r&gt;=1有<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>&lt;X0,...,Xn-1,Xn,...,Xn+r&gt; = &lt;X0,...,Xn-1,&lt;Xn,...,Xn+r&gt;&gt;<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>=<wbr><wbr>&lt;X0,...,Xn-1,Xn+1/&lt;Xn+1,...,Xn+r&gt;&gt;.<br><wbr><wbr><wbr><wbr><wbr>特别地有<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>&lt;X0,...,Xn-1,Xn,Xn+1&gt; = &lt;X0,...,Xn-1,Xn+1/Xn+1&gt;<br><wbr><wbr><wbr><wbr><wbr>注:用该定理可以求连分数的值</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>

(2)对于连分数数数列 <X0,...Xn> 有递推关系:
<wbr><wbr><wbr><wbr><wbr>Pn = XnPn-1+Pn-2;<br><wbr><wbr><wbr><wbr><wbr>Qn = XnQn-1+Qn-2;<br><wbr><wbr><wbr><wbr><wbr>定义:<wbr>P-2 = 0; P-1 = 1; Q-2 = 1; Q-1 = 0;<br><wbr><wbr><wbr><wbr><wbr>所以:<wbr>P0 = X0; Q0 = 1; P1 = X1X0+1; Q1 = X1;<br><wbr><wbr><wbr><wbr><wbr>特别地:当 Xi=1 时, {Pn}, {Qn}为Fbi数列</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>

(3)对于连分数数数列 <X0,...Xn>
<wbr><wbr><wbr><wbr>当n&gt;= 1时，我们有PkQk-1 = Pk-1Qk = (-1)^k<br><wbr><wbr><wbr><wbr>当n&gt;=2时， 我们有PkQk-2 = Pk-2Qk = (-1)^(k - 1) * xk</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>

(4) 所有有理数都可以表示成有限连分数

(5)pell方程: x^2+ny^2=+-1的解法:
<wbr><wbr><wbr><wbr><wbr>若n是平方数,则无解, 否则:<br><wbr><wbr><wbr><wbr><wbr>先求出sqrt(n)的连分数序列&lt;x0,x1..xn&gt; 其中xn = 2*x0;<br><wbr><wbr><wbr><wbr><wbr>对于 x^2+ny^2=-1<br><wbr><wbr><wbr><wbr><wbr>若n为奇数,则 x=Pn-1, y=Qn-1; n为偶数时无解<br><wbr><wbr><wbr><wbr><wbr>对于 x^2+ny^2=1<br><wbr><wbr><wbr><wbr><wbr>若n为偶数,则 x=Pn-1, y=Qn-1; n为奇数时x=P2n-1, y=Q2n-1<br><wbr><wbr><wbr><wbr><wbr>注:以上说的解均为最小正解</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>